JOURNALコラム

【マーケターズコラムVol.4】論理的思考の第一歩!「パラドックス」について考えてみる
ビジネスシーンにおいては、
よく「論理的思考(ロジカルシンキング)」が
重要だと言われます。
感覚的な判断ではなく、
論理的な帰結を求められるのですが、
苦手に思っている方も多いのではないでしょうか。
マーケティングにおいても
論理的思考のためのフレームワークは
たくさん用意されています。
例えばロジックツリー。
例えばMECE思考。
ただ、使い慣れていないと
フレームワークの型通りにすることに
終始してしまうことも少なくありません。
論理的思考を鍛える方法は
いくつか存在しますが、
今回はその第一歩として、
「パラドックス」について考えていく、
というテーマでお話ししようと思います。
難しく考えるというよりも、
楽しく考えてもらえる内容なので、
ぜひ最後まで読んでみてくださいね。
論理的思考はいろんな場面で役立つ

「パラドックス」についてお話しする前に、
論理的思考がいかに重要か、
ということに触れておこうと思います。
先述した通り、
ビジネスでは論理的思考が求められる場面は
非常に多くあります。
実施したプロモーションがなぜ成功したのか、
あるいはなぜ失敗したのか。
そこには「要因」が存在しており、
その「要因」によって「結果」が
起こっていることになります。
この「因果関係」を把握することで、
次の一手が導き出されます。
論理的思考は数学的発想(理系的発想)と
思われることもありますが、
もちろんそんなことはありません。
大学入学共通テストでは、
国語で毎回論説文が出題されますし、
設問には因果関係を問うものが多いです。
日本史や世界史などもそうですね。
歴史を学ぶ際のポイントとして、
ある事象がなぜ起こったのか、
因果関係を把握してくと
理解が深まるといわれています。
当時の世相、発端となった事件など
物語として理解することで
記憶に定着しやすくなります。
「因果関係」を意識することで、
様々なことに「なんでだろう?」と
考えられるようになります。
それは興味を広げることにつながり、
多くの知識や情報の習得にもつながります。
人とのコミュニケーションでも
活きてくるものなので、
論理的思考はビジネス以外の場面でも
大いに役立つといえるでしょう。
「パラドックス」とは何か
前置きが長くなってしまいましたが、
今回のテーマである「パラドックス」について
話していこうと思います。
「パラドックス(paradox)」は
ギリシャ語の「para(超えた、外れた)」と
「doxa(概念)」という言葉に由来しています。
辞書的な意味合いで説明すると、
一見正しそうに思える理論の中に、
明らかに誤りが含まれていたり、
受け入れがたい結論につながったりする
状態を表しています。
これだけだとちょっとわかりにくいですね。
もう少しかみ砕いてお話しすると、
正しい方法で物事を考えていったものの、
その結論に矛盾が生じてしまったり、
一般的に正しいと思われていることとは
異なる・反する結論になってしまったりすることを
パラドックスと呼びます。
分かりやすい例を挙げてみましょう。
パラドックスの命題として
「自己言及のパラドックス」というものがあり、
最も有名なものに「嘘つきのパラドックス」
というものがあります。
「私は嘘つきだ」という人は
本当に「嘘つき」でしょうか?
少し考えてみましょう。
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
仮に「私は嘘つきだ」ということが正しい場合、
その人は本当に「嘘つき」という結論になるので、
「嘘つきである」と正しいことを言っている時点で
話が矛盾してしまいます。
一方その主張が「嘘」だった場合、
その人は「嘘つき」ではなくなりますが、
最初の主張では「嘘つき」と言っているので
これもまた矛盾してしまいます。
このように、どのように考えを進めていっても
最初の条件と反する結論が生まれるため、
この命題は「論理的な矛盾」を孕んだ
パラドックスとなります。
「全能のパラドックス」を論理的に考える

他にも例を挙げてみましょう。
あなたは「全知全能」というものが
この世に存在すると思いますか?
また少し考えてみてください。
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
論理的な思考を突き詰めていくと、
「全知全能」は存在しない、
という結論になります。
なぜこの結論になるのでしょうか?
具体的なイメージを持って考えると、
分かりやすくなります。
「全知全能」とはすなわち、
知らないことは一つもなく、
できないことは何もない、
ということになります。
何でもできるということは、
例えば「無」から「有」を生み出すことも
できるわけです。
とすれば、
「自分を存在しないものにする」
こともできてしまうわけです。
ただ、そうすると全知全能は
「存在しない」という結論になります。
他のパターンで言えば、
「四角い円」を生み出すこともできません。
なぜなら「円」は四角では構成されないからです。
このように、
「全知全能」であってもできないことはあり、
それはつまり「全知全能」ではない、
という結論にたどり着きます。
これを「全能のパラドックス」と呼びます。
ただ、これはあくまで論理学的に考えた
結論でしかありません。
例えば「全知全能」は論理を超越した
存在である、と仮定すれば、
先ほどの矛盾した内容が
成立することになります。
この命題は、
論理学者、哲学者、神学者など
立場によって意見も分かれています。
少し複雑な話ですが、
あくまで論理的な思考をしていくと
このパラドックスに気付ける、
というわけですね。
モンティ・ホール問題に見るパラドックス

他に有名なパラドックスの例として、
「モンティ・ホール問題」というものがあります。
これは1960年代にアメリカで放送された
モンティ・ホールが司会者を務める
『Let’s make a deal』という番組の中で
行われたゲームに由来する論争です。
実際の問題を見てみましょう。
プレーヤーの前に閉じた3つのドアがあって、
1つのドアの後ろには景品の新車が、
2つのドアの後ろには、
はずれを意味するヤギがいる。
プレーヤーは新車のドアを当てると
新車がもらえる。
プレーヤーが1つのドアを選択した後、
司会のモンティが残りのドアのうち
ヤギがいるドアを開けてヤギを見せる。ここでプレーヤーは、最初に選んだドアを、
残っている開けられていないドアに
変更してもよいと言われる。
ここでプレーヤーはドアを変更すべきだろうか?
あなたはこれを「変更するべき」と
考えますか?
それとも「変更しないべき」と
考えますか?
少し考えてみてください。
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
この答えは、
「変更するべき」となります。
扉を変えない場合、
正解の確率は1/3ですが、
扉を変えると正解の確率は
2/3になるからです。
しかし、この回答に対しては
多くの論争が巻き起こることになりました。
なぜなら、普通に考えると、
残っている扉は2つであり、
扉を変えようが変えまいが
正解の確率は1/2で
変えるメリットがない、
という結論になるからです。
これだけだと分かりづらいので、
実際に確率を計算してみましょう。
まずは扉にそれぞれ
「A」「B」「C」という名前を付けます。
そして、最初に挑戦者が選ぶ扉を
便宜上「A」としておきます。
この時起こるパターンは
①正解が「A」の扉、司会者が「B」の扉を開ける
②正解が「A」の扉、司会者が「C」の扉を開ける
③正解が「B」の扉、司会者が「C」の扉を開ける
④正解が「C」の扉、司会者が「B」の扉を開ける
の4パターンとなります。
それぞれのパターンは
確率で計算すると
①②が1/6
③④が1/3ずつで
発生します。
①②について、
正解が「A」の扉である確率は1/3で、
司会者が残りのどちらを開けるかは
それぞれ1/2ずつなので、
①も②も1/3×1/2=1/6です。
③④は司会者が外れを選ぶときに
挑戦者が選んだ「A」の扉を
空けることはありません。
そのため正解の扉が「B」、「C」で
ある確率と等しいので、
どちらも1/3ずつとなりますよね。
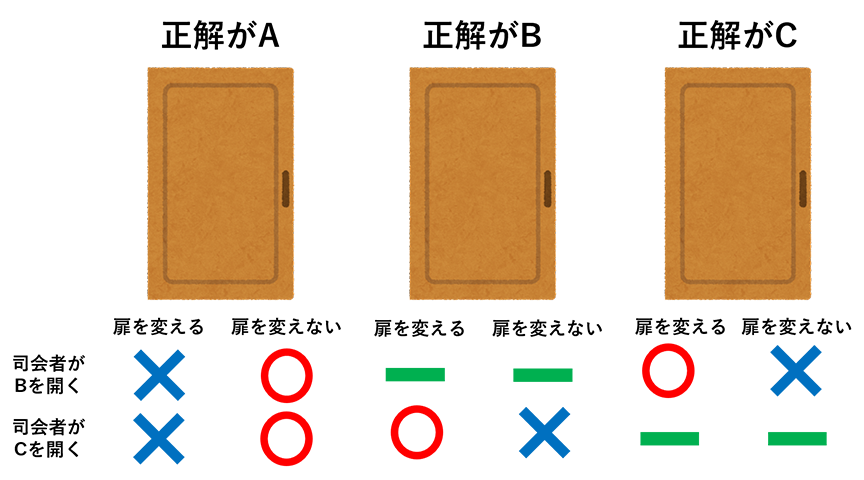
① では扉を変えると外れてしまい、
扉を変えないと正解となります。
②のパターンも全く同じですね。
③④のパターンは反対に
扉を変えると正解で、
変えないと外れてしまいます。
そうすると、
扉を変えた場合に正解する確率は
1/3+1/3=2/3
変えない場合に正解する確率は、
1/6+1/6=1/3
となります。
つまり、扉を変えた方が
変えない時に比べて2倍も
正解しやすくなるというわけですね。
数学的に考えるのが苦手な方は、
扉の数を増やして考えてみると
分かりやすくなります。
問題では3つの扉でしたが、
100個扉があると考えてみましょう。
100個の扉があり、挑戦者は
その中から1つの扉を選びます。
司会者は残りの99個の扉から
98個の不正解の扉を開けます。
その後、挑戦者は
残りの2つの扉から
好きな方を選べるとします。
この時扉を変えるべきでしょうか、
変えないべきでしょうか?
こうなってくると、
最初に100個あるうちから
選んだ扉よりも、
司会者が開けずに残された
もう1つの扉の方が
正解なのでは?
と感じますよね。
100個という極端な例ではありますが、
考え方は3つの時と同じなので、
やはり扉は変えるべき、
というのが論理的な結論になります。
パラドックスは論理的思考能力を引き上げる

ここまで様々なパラドックスの例を
見てきました。
他にも有名なものはたくさんあり、
「抜き打ちテストのパラドックス(死刑囚のパラドックス)」
「誕生日のパラドックス」
「無限のパラドックス」
などは考えてみると面白いです。
少しクイズ的にご紹介していきましたが、
パラドックスの命題はどれも
論理的思考をしていくことで
面白さが分かるものばかりです。
論理的思考を養っていくにあたって、
非常に取り組みやすいものでもあるので、
もし論理的思考が苦手だと思うのであれば、
まずはパラドックスについて
考えてみるととっつきやすいかもしれませんね。
教育関連のプロモーションについては、私たちCCG MANABIにお任せください。
お問い合わせから、お気軽にご連絡ください。